Non-Linear Functions for Diminishing Returns

Non-linear functions are very useful in solving business problems that deal with optimization. Particularly in the marketing space, I often work on problems with the objective of:

  • 1. Estimating the relationship between dollars spent and revenue earned - (diminishing returns)
  • 2. Estimating the decaying impact of advertisement over time (exponential relationship.)

This note, introduces four mathematical functions that provide functional forms to model various non-linear problems. The functions are:

  • 1. Power Function
  • 2. Logarithmic Growth Function
  • 3. Negative Exponential Function
  • 4. Michaelis Menten Function

1. Power Function

The power function can be used to model non-linear relationships with a lot of flexibility due to the beta parameter. Mathematically, it is represented as:

$$ f(x) = \alpha * x^{\beta} $$

where:
$\alpha$: is a scalar parameter for scaling the power function
$\beta$: define the non-linear form with varying values.

The code below implements an example of the power function with varying levels of $beta$ values = [ .001, 1, 3] 

import numpy as np 
import seaborn as sns
import matplotlib.pyplot as plt 

%matplotlib inline
%config InlineBackend.figure_format = 'retina'
def power_function(x, alpha, beta):
    return alpha * (x)**beta

x_vals = np.linspace(5, 50, 30)

# parameters alpha =20 and beta = .001, 1, 3
pars = list(zip([20 , 20, 20],[ .001, 1, 3]))
y_vals = {'α = {}, β = {}'.format( pars[i][0], pars[i][1]) : power_function(x_vals, pars[i][0], pars[i][1],) for i,value in enumerate(pars)}
## Visualize the plot
fix, ax = plt.subplots(1, 3, figsize=(20,6))

ax[0].plot(x_vals, y_vals['α = 20, β = 0.001'], label='α = 20, β = 0.001')
ax[0].set_title("Power Functions: α = 20, β = 0.001")
ax[0].legend()

ax[1].plot(x_vals, y_vals['α = 20, β = 1'], label='α = 20, β = 1')
ax[1].set_title("Power Functions: α = 20, β = 1")
ax[1].legend()

ax[2].plot(x_vals, y_vals['α = 20, β = 3'], label='α = 20, β = 3')
ax[2].set_title("Power Functions: α = 20, β = 3")
ax[2].legend()

plt.tight_layout()
plt.show()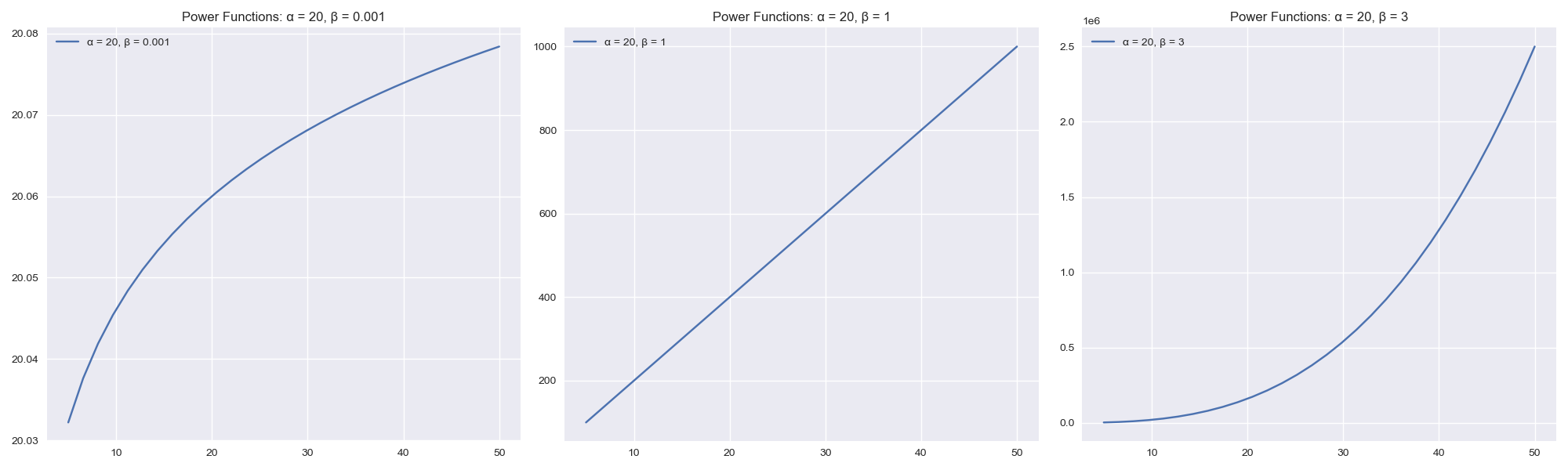
Power Function with Varying Betas

2. Logarithmic Growth Function

The logarithmic growth function is another alternative that can fit a diminishing returns property. The functional form of the logarithmic growth model is:

$$ f(x) = \alpha + \beta * ln(x)$$

where:
$\alpha$: the intercept for the function
$\beta$: tuning parameter for the slope of the growth function

Below we see an example of the logarithmic growth functions with varying betas and their response curves.

def log_growth(alpha, beta, x):
    return alpha + beta*np.log(x)

x_vals = np.linspace(1, 50, 20 )
pars = list(zip([20 , 20, 20],[10, 30, 50]))

x_vals = np.linspace(1, 50, 20 )
y_vals = { 'α = {}, β = {}'.format( pars[i][0], 
            pars[i][1]):log_growth(pars[i][0], pars[i][1],x=x_vals) for i,value in enumerate(pars)}
## Visualize the plot
fig, ax = plt.subplots(1, 3, figsize=(20,6))

ax[0].plot(x_vals, y_vals['α = 20, β = 10'], label='α = 20, β = 10')
ax[0].set_title("Log Growth Functions: α = 20, β = 10")
ax[0].legend()

ax[1].plot(x_vals, y_vals['α = 20, β = 30'], label='α = 20, β = 30')
ax[1].set_title("Log Growth Functions: α = 20, β = 30")
ax[1].legend()

ax[2].plot(x_vals, y_vals['α = 20, β = 50'], label='α = 20, β = 50')
ax[0].set_title("Log Growth Functions: α = 20, β = 50")
ax[2].legend()

plt.tight_layout()
plt.show()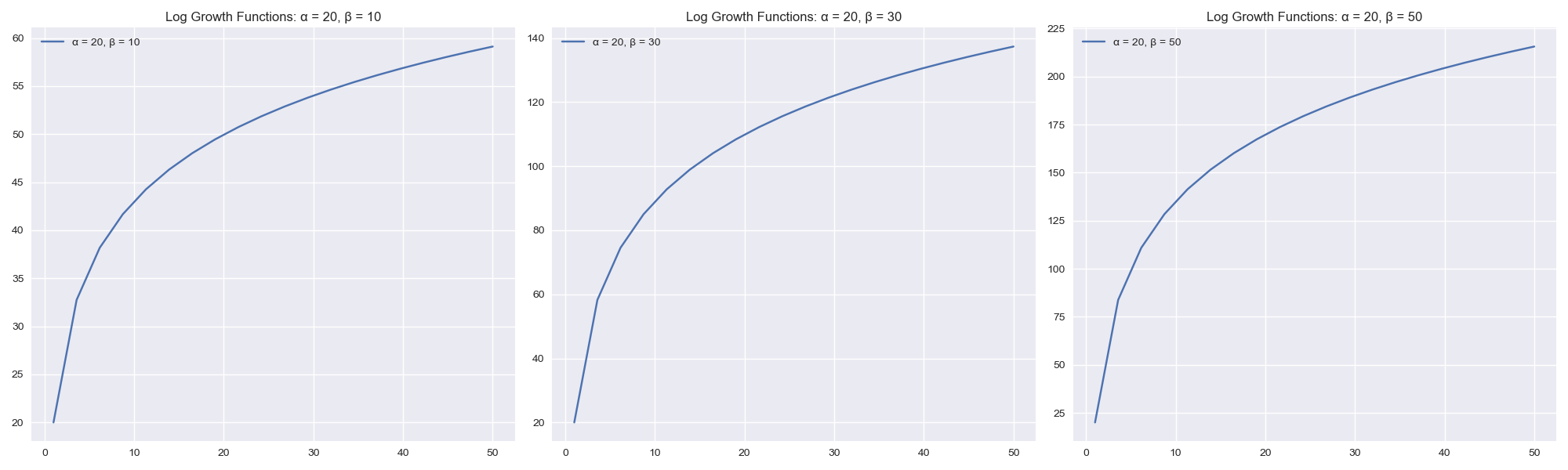
Logarithmic Growth Function with Varying Betas

3. Negative Exponential Function

Another useful family of functions for non-linear models is the exponential family which models exponential growth and decay between two variables. For diminishing returns, we are interested in negative exponential growth. The mathematical function of negative exponential growth is:

$$ f(x) = \alpha * (1 - exp^{(-\beta x)}) $$

where:
$\alpha$: tuning parameter for scale
$\beta$: tuning parameter for exponential trend

For diminishing returns curve, we need $\beta > 0$ must be set as the condition. In the code below, we explore the various conditions. We try the following parameters:

$\alpha=7$
$\beta=.003$ ~ linear
$\beta=.1$ ~ diminishing returns
$\beta=.2$ ~ strong diminishing returns 

def negative_exponential(alpha, beta, x):
    return alpha * (1 - np.exp(-beta * x) )


x_vals = np.linspace(1, 50, 20 )
pars = list(zip([7,7,7],[.003, .1, .5]))

x_vals = np.linspace(1, 50, 20 )
y_vals = { 'α = {}, β = {}'.format( pars[i][0],
            pars[i][1]): negative_exponential( pars[i][0], pars[i][1], x=x_vals) for i,value in enumerate(pars)}
## Visualize the plot
fig, ax = plt.subplots(1, 3, figsize=(20,6))

ax[0].plot(x_vals, y_vals['α = 7, β = 0.003'], label='α = 7, β = 0.003')
ax[0].set_title('Negative Exponential Function: α = 7, β = 0.003')
ax[0].legend()

ax[1].plot(x_vals, y_vals['α = 7, β = 0.1'], label='α = 7, β = 0.1')
ax[1].set_title('Negative Exponential Function: α = 7, β = 0.1')
ax[1].legend()

ax[2].plot(x_vals, y_vals['α = 7, β = 0.5'], label='α = 7, β = 0.5')
ax[2].set_title('Negative Exponential Function: α = 7, β = 0.5')
ax[2].legend()

plt.tight_layout()
plt.show()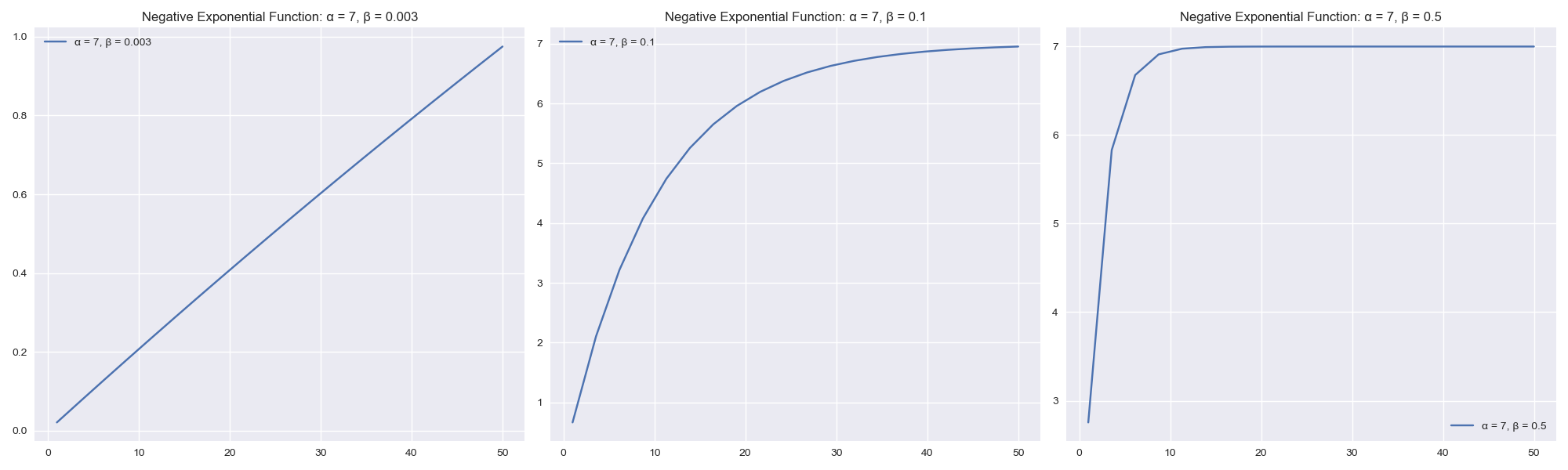
Negative Exponential Function with Varying Betas

4. Michaelis-Menten Function

Michaelis-Menten function that is finds its root in biology looking at Enzyme reaction. The functional form can be used for modeling diminishing returns with constraints on parameters. The mathematical definition of the function is:

$$ f(x) = \frac {\alpha * x } { 1 + \beta * x} $$

where:
$\alpha$: scaling parameter for x
$\beta$: tuning parameter for diminishing returns.

To return a diminishing returns form, we need to constrain $\beta \geq 0$. In the example below, we see variations of these functions based on different $\beta$ values. We visualize the following values:

$\alpha=7$
$\beta=.01$ ~ linear to dim returns
$\beta=.05$ ~ diminishing returns
$\beta=.1$ ~ diminishing returns
$\beta=1$ ~ strong diminishing returns 

def michaelis_menten(alpha, beta, x):
    return (alpha*x)/(1 + beta*x)

pars = list(zip([7,7,7,7],[.01, .05, .1, 1]))

x_vals = np.linspace(1, 50, 20 )
y_vals = { 'α = {}, β = {}'.format( pars[i][0], 
            pars[i][1]):michaelis_menten(pars[i][0],pars[i][1],x=x_vals) for i,value in enumerate(pars)}
fig, ax = plt.subplots(1, 4, figsize=(25,7))

ax[0].plot(x_vals, y_vals['α = 7, β = 0.01'], label='α = 7, β = 0.01')
ax[0].legend()
ax[0].set_title('Michaelis-Menten Function:  α = 7, β = 0.01', fontsize=15)

ax[1].plot(x_vals, y_vals['α = 7, β = 0.05'], label='α = 7, β = 0.05')
ax[1].set_title('Michaelis-Menten Function:  α = 7, β = 0.05', fontsize=15)
ax[1].legend()

ax[2].plot(x_vals, y_vals['α = 7, β = 0.1'], label='α = 7, β = 0.1')
ax[2].set_title('Michaelis-Menten Function:  α = 7, β = 0.1', fontsize=15)
ax[2].legend()

ax[3].plot(x_vals, y_vals['α = 7, β = 1'], label='α = 7, β = 1')
ax[3].set_title('Michaelis-Menten Function:  α = 7, β = 1', fontsize=15)
ax[3].legend()

plt.tight_layout()
plt.show()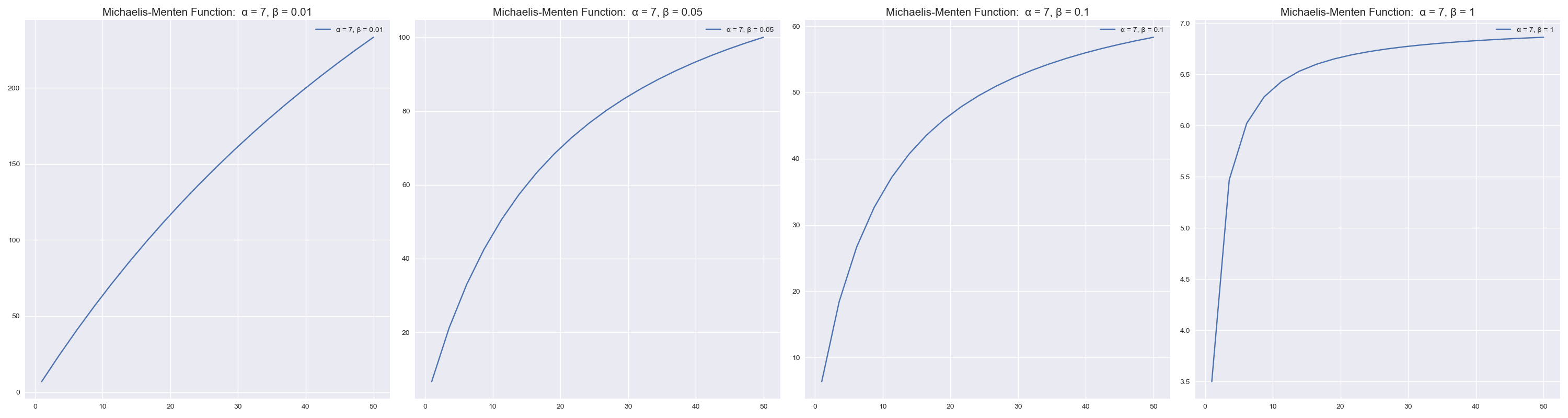
Michaelis Menten Function with Varying Betas

The Michaelis-Menten function is commonly used in enzyme kinetics, while the Hill function is used to model the cooperative binding of ligands to proteins. However, they can also be applied to various other fields, including economics, finance, and marketing, to model relationships that exhibit the property of diminishing returns.